Pergel ve Cetvel ile İmkansız Çizimler – Can Numan

Bu yazımızda Antik Yunan’dan yadigar pergel ve cetvel inşalarını inceleyeceğiz ve çeşitli problemlerin çözümsüzlüğünü göstereceğiz. Yazının içeriğinin lise seviyesinde Öklit geometrisi görmüş herkes için anlaşılır olacağını umuyorum. İlgileneceğimiz problemler şunlar olacak. Pergel ve cetvel ile;

Bir çember verildiğinde bu çemberle aynı alana sahip bir kare çizmek.
Birim uzunluk verildiğinde $\sqrt[3]{2}$ uzunluğunu inşa etmek.
Bir açı verildiğinde bu açıyı üçe bölmek.
Düzgün çokgen çizmek.

Amacımız sadece pergel ve cetvel kullanarak ilk üç problemin çözülemeyeceğini göstermek ve üçüncü problemin çözülebilmesi için gerek ve yeter bir koşul bulmak.

Pergel ve cetvel inşası nedir?

Noktasal bir uca sahip bir pergel ve işaretsiz bir cetvelimiz olsun. Burada cetvelin işaretsiz olması önemli zira cetveli uzunluk ölçmek için değil sadece ve sadece elimizdeki noktaları birleştiren doğruları çizmek ve çizdiğimiz doğruları istediğimiz kadar uzatabilmek için kullanacağız.

Amacımız, elimizdeki ideal pergel ve işaretsiz cetveli kullanarak sonlu adım sonunda hangi uzunlukları, açıları ve düzgün çokgenleri inşa edebileceğimizi bulmak. Yapacağımız inşalar hakkında bir şeyler kanıtlamak istediğimiz için -doğal olarak- soruyu matematiksel bir zemine oturtmalıyız.

Bunun ilk adımı olarak da pergel ve cetvel kullanarak bir inşa gerçekleştirdiğimizde inşanın her adımında hangi işlemlerin yapılabileceğini tanımlamalıyız.

Bir pergel ve cetvel inşasının her adımında aşağıdaki temel işlemlerden birini yapabiliyoruz:

Elimizdeki iki noktadan geçen doğruyu çizmek.
Elimizdeki iki noktanın birini merkez alan ve diğerinden geçen çemberi çizmek.
Elimizdeki paralel olmayan iki doğrunun kesiştiği noktayı bulmak.
Elimizdeki bir doğrunun ve bir çemberin -eğer kesişiyorlarsa- kesişim noktalarını bulmak.
Elimizdeki iki çemberin -eğer kesişiyorlarsa- kesişim noktalarını bulmak.

Bu çizimlerin ideal bir pergel ve işaretsiz bir cetvel ile nasıl gerçekleştirilebileceği açık olmalı. Burada dikkat edilmesi gereken nokta bu işlemlerin hepsinin daha önceki adımlarda elde edilmiş noktalar, doğrular ve çemberler üzerinden tanımlanması. Yani bu temel işlemleri kullanarak bir pergel ve cetvel inşası gerçekleştirebilmek için bize ilk başta bir şeyler verilmiş olması gerekiyor!

Pergel ve cetvel ile gerçekleştirilebilen bazı operasyonlar

İlk bakışta yukarıdaki temel işlemleri uygulayarak fazla karmaşık şeyler yapamayacağımızı düşünebilirsiniz. Eğer böyle düşünüyorsanız, yanılıyorsunuz!

Yazının bu bölümünde pergel ve cetvel ile gerçekleştirilebilen bazı temel operasyonları göreceğiz. Bu operasyonların çoğunu yazının daha sonraki bölümlerinde -üstü kapalı olarak- kullanacağımız için her bir operasyonun nasıl yapıldığını anlamanız yazının kalanının anlaşılabilirliği açısından önemli.

Yazının bu bölümünü okurken anlatılacak çizimleri Euclid the Game isimli sitedeki uygulamayı kullanarak kendiniz de yapabilirsiniz.

Bir doğru parçasının orta noktasını bulmak: Diyelim ki uç noktaları A ve B olan bir doğru parçası verildi. Pergelimizi |AB| kadar açtıktan sonra merkezi A ve B noktaları olan iki çember çizelim. Bu çemberler iki noktada kesişecektir; bu noktalar C ve D noktaları olsun. C ve D noktalarını birleştiren doğrunun verilen doğru parçasını kestiği nokta bu doğru parçasının orta noktası olacaktır. İlgili Euclid the Game bölümü.
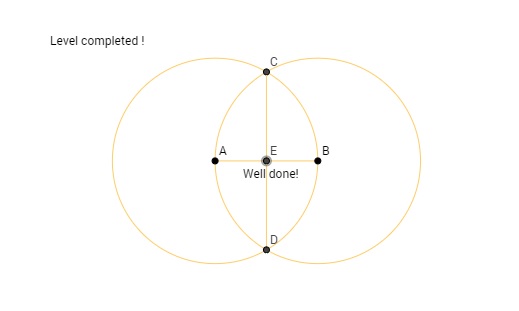
Verilen bir açıyı ikiye bölmek: Diyelim ki iki ışın arasında kalan bir açı verildi. Bu ışınlardan biri üzerinde verilen ikinci bir noktamız olsun. Işınların kesiştiği noktaya A, ışınların biri üzerindeki ikinci noktaya da B diyelim. A merkezli |AB| yarıçaplı çemberi çizelim ve diğer ışını kestiği noktayı işaretleyelim, bu noktaya C noktası diyelim. B ve C noktalarını merkez alan ve |BC| yarıçaplı çemberleri çizelim. Bu çemberlerin kesiştiği iki noktadan birisini alalım. Bu nokta D noktası olsun. A ve D noktalarından geçen doğru BAC açısını ikiye bölecektir. İlgili Euclid the Game bölümü.
Verilen bir doğruya bu doğru üzerindeki bir noktadan dik çizmek: Bir doğru ve bu doğru üzerinde bir A noktası verildiğini varsayalım. Bu doğru üzerinde ikinci bir B noktası verilsin. A merkezli ve |AB| yarıçaplı çemberi çizerek bu çemberin doğruyla kesiştiği noktayı bulalım. Bu nokta C noktası olsun. B ve C noktalarını merkez alan |BC| yarıçaplı iki çember çizerek bu çemberlerin kesişim noktalarını bulalım. Bu noktaları birleştiren doğru A noktasından geçecek ve bize verilen ilk doğruya dik olacaktır. İlgili Euclid the Game bölümü.
Verilen bir doğruya bu doğru üzerinde olmayan bir noktadan dik çizmek: Diyelim ki elimizde bir doğru ve bu doğru üzerinde olmayan bir B noktası var. Bu doğru üzerinde olan bir A noktası verilsin. B merkezli ve |BA| yarıçaplı çemberi çizdikten sonra bu çemberin verilen doğruyla kesiştiği noktaya C diyelim. Birinci operasyonu kullanarak AC doğru parçasının orta noktasını bulalım. Bu nokta D noktası olsun. BD doğrusu verilen doğruya diktir. İlgili Euclid the Game bölümü.
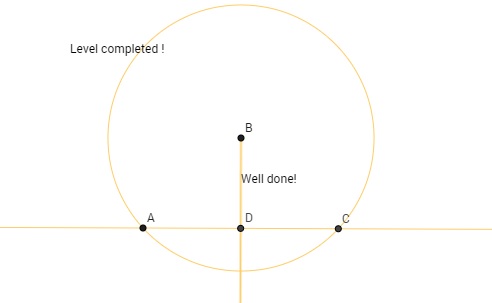
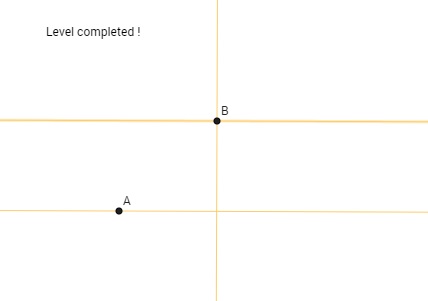
Verilen bir doğruya üzerinde olmayan bir noktadan paralel çizmek: Diyelim ki elimizde bir doğru ve bu doğru üzerinde olmayan bir B noktası var. Dördüncü operasyonu kullanarak B noktasından geçen ve verilen doğruya dik olan bir doğru çizelim. Bu elde ettiğimiz yeni doğruya ve B noktasına üçüncü operasyonu uygularsak, verilen ilk doğruya paralel ve B noktasından geçen bir doğru elde edeceğiz. İlgili Euclid the Game bölümü.
Verilen bir noktadan verilen bir doğru parçasıyla aynı uzunlukta ve aynı doğrultuda bir doğru parçası çizmek: Diyelim ki uç noktaları A ve B olan bir doğru parçası ve bu doğru parçası üzerinde olmayan bir C noktası verildi. Beşinci operasyonu kullanarak A ve B noktalarından geçen doğruya paralel olan ve C noktasından geçen bir doğru çizebiliriz. Bu doğru L doğrusu olsun. Benzer şekilde, A ve C noktalarından geçen doğruyu çizdikten sonra bu doğruya paralel olan ve B noktasından geçen bir doğru da çizebiliriz. Bu doğru da K doğrusu olsun. K ve L doğrularının kesiştiği nokta D noktası olsun. CD doğru parçası AB ile aynı doğrultuda ve aynı uzunluktadır. İlgili Euclid the Game bölümü.

Euclid the Game oyununu bitirmenizi tavsiye ediyorum zira ufuk açıcı bir oyun. Yazının devamında yapacaklarımız için yukarıda listelenen operasyonlar yeterli olduğundan dolayı pergel ve cetvelle gerçekleştirilebilecek diğer işe yarar operasyonları atlıyorum.

İnşa edilebilir sayılar

Hatırlayın, bir pergel ve cetvel inşasında izin verdiğimiz işlemlerin hepsi daha önceki adımlarda elde edilmiş noktalar, doğrular ve çemberler üzerinden tanımlanıyordu. Dolayısıyla herhangi çizim yapmaya başlayabilmek için bize ilk başta bir şeylerin verilmiş olması gerekiyor.

Çizimlerimizde ilk başta düzlem üzerinde işaretlenmiş iki tane nokta olduğunu varsayacağız. Bu noktalar arasındaki uzaklığı da birim uzunluk olarak alacağız.

Soru: Pergel ve cetvel kullanarak hangi uzunlukları inşa edebiliriz?

Yani aralarındaki uzaklık birim uzunluk olan iki nokta ile başlarsak izin verilen temel işlemleri uygulayarak sonlu adım sonunda hangi uzunlukları inşa etmek mümkün? Burada bir $r$ uzunluğunu inşa etmekten kastımız, inşamızın sonunda aralarındaki uzaklık $r$ olan iki nokta elde edebilmek.

Tanım: Bir $r$ gerçel sayısına inşa edilebilir diyelim ancak ve ancak $|r|$ uzunluğunu bir pergel ve cetvel inşası sonucunda elde edebiliyorsak.

Şimdi hangi sayıları inşa edebileceğimi hakkında düşünmeye başlayalım. Doğal sayıların -dolayısıyla tam sayıların- hepsi inşa edilebilirdir zira başlangıçta verilen iki noktadan geçen doğruyu çizdikten sonra her biri sonrakinin merkezinden geçen art arda çemberler çizerek tüm doğal sayıları elde edebiliriz. Mesela $4$ sayısı inşa edilebilirdir zira

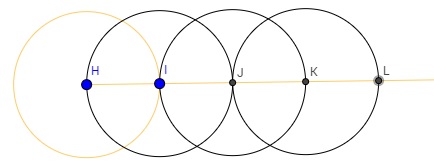
Tam sayılar inşa edebilir olduğuna göre üçgen benzerliğini kullanarak rasyonel sayıların da inşa edilebilir olduğunu şu şekilde kolayca gösterebiliriz. Diyelim ki bir $\frac{m}{n}$ rasyonel sayısının inşa edilebilir olduğunu göstermek istiyoruz. Kenarı birim uzunlukta olan bir eşkenar üçgen çizelim. Bu üçgenin iki kenarını içeren ışınları çizdikten sonra bu ışınlar üzerinde $|m|$ ve $|n|$ uzunluklarını elde edelim. Elde ettiğimiz bu uzunluklara sahip doğru parçalarının uç noktaları birleştiren doğruyu çizelim. Bu doğruya L doğrusu diyelim. Eşkenar üçgenin $|m|$ ve $|n|$ uzunluklarını veren doğru parçalarıyla kesişmediği iki köşesinden L doğrusuna paraleller çizersek, bu doğruların eşkenar üçgenin ilgili kenarlarını kestiği noktaların uzunlukları benzerlikten dolayı $\frac{|m|}{|n|}$ ve $\frac{|n|}{|m|}$ olacaktır. Mesela $\frac{3}{5}$ rasyonel sayısı inşa edilebilirdir zira

Öte yandan rasyonel olmayan uzunlukları da inşa edebileceğimizi biliyoruz. Zira birim eşkenar üçgen çizebildiğimize göre, bu üçgenin bir kenarına dik inerek $\frac{\sqrt{3}}{2}$ uzunluğunu elde edebiliriz. Başka bir örnek verelim. Biraz uğraşla pergel ve cetvelle birim kare inşa edilebileceğini gözlemleyebilirsiniz. Ancak bu durumda, bu karenin köşegeninin uzunluğu olan $\sqrt{2}$ sayısı inşa edilebilir bir sayıdır.

İnşa edilebilir sayıları karakterize etmek

Demek ki inşa edilebilir sayılar kümesi rasyonel sayıları içeren ancak rasyonel sayılardan daha büyük bir küme. Şimdi bu kümenin cebirsel yapısını anlamaya çalışalım.

Teorem: Eğer $a$ ve $b \neq 0$ inşa edilebilir sayılarsa, o zaman $a+b, a-b, ab$ ve $\frac{a}{b}$ sayıları da inşa edilebilirdir.

Bu teoremin kanıtını okuyucuya egzersiz olarak bırakıyorum zira kanıt çok zor değil. Yazının bir önceki bölümündeki operasyonların nasıl yapılacağını boşuna göstermedik!

Bu yazı GM serisinde olduğu için fazla teknik terimler kullanmak istemiyorum ama bilenler için vurgulama gereği duyuyorum; yukarıdaki teorem bize inşa edilebilir sayıların gerçel sayıların bir alt cismi olduğunu söylüyor. Peki bu cismin başka ne özellikleri var?

Teorem: Eğer $a > 0″ width=”45″ height=”14″ srcset=”https://s0.wp.com/latex.php?latex=a+%3E+0&bg=ffffff&fg=4c4c4c&s=1&c=20201002&zoom=2 1.5x”> inşa edilebilir bir sayıysa, o zaman <img decoding=$ sayısı da inşa edilebilirdir.
Kanıt: $a$ inşa edilebilir pozitif bir sayı olsun. Bu durumda $a+1$ sayısı da inşa edilebilirdir. Şimdi uzunluğu $a+1$ olan bir doğru parçası (şekildeki HJ doğru parçası) çizdikten sonra bir numaralı operasyon yardımıyla bu doğru parçasının orta noktasını bulalım (şekildeki M noktası). Daha sonra merkezi bu nokta olan $\frac{a+1}{2}$ yarıçaplı çemberi çizelim. $a$ inşa edilebilir olduğuna göre çemberin çapını $a$ ve $1$ şeklinde bölecek noktayı bir pergel ve cetvel inşasıyla elde edebiliriz. Bu nokta I noktası olsun. Üçüncü operasyonu kullanarak I noktasından geçen ve çapa dik olan bir doğru çizelim. Bu doğrunun çemberle kesiştiği nokta N noktası olsun. Bu durumda NI doğru parçasının uzunluğu $\sqrt{a}$ olacaktır. (Son basamaktaki iddianın neden doğru olduğunu anlamak için HNJ üçgeninin bir dik üçgen olduğunu fark edip bu üçgende Öklit bağıntısını uygulayın.) $\blacksquare$

Demek ki inşa edilebilir gerçel sayıların oluşturduğu cisim pozitif elemanların kareköklerini alma işlemi altında kapalı. Daha teknik terimlerle konuşmak gerekirse, inşa edilebilir sayılar Öklityen bir cisim. Birazdan inşa edilebilir sayıların rasyonel sayıları içeren, aritmetik işlemler ve pozitif elemanların karekökünü alma işlemi altında kapalı olan gerçel sayıların en küçük alt kümesi olduğunu göreceğiz.

Hatırlayın, pergel ve cetvel inşalarını yapabilmemiz için düzlemde bize aralarındaki uzaklığı birim uzaklık aldığımız iki nokta verilmişti. Şimdi bu noktaların sırasıyla $(0,0)$ ve $(1,0)$ koordinatlarına sahip olduğu bir koordinat sistemi hayal edelim.

$r$ inşa edilebilir bir sayı olsun. İnşa edilebilirliğin tanımı gereği öyle bir pergel ve cetvel inşası vardır ki bu inşa sonunda elde ettiğim noktalar içerisinde aralarındaki uzaklık $|r|$ olan iki nokta bulabiliriz. Ancak aralarındaki uzaklık $|r|$ olan iki nokta bulabiliyorsak, altı numaralı operasyonu uygulayıp bir ucu $(0,0)$ olan $|r|$ uzunluğunda bir doğru parçası da elde edebiliriz. Bu durumda $(0,0)$ noktasını merkez alan $|r|$ yarıçaplı çemberi çizip koordinat eksenleriyle kesiştirerek $(|r|,0)$ noktasını elde edebiliriz.

Demek ki $r$ inşa edilebilir bir sayıysa, öyle bir pergel ve cetvel inşası vardır ki bu inşanın sonunda koordinatları $(|r|,0)$ olan nokta elde edilebiliyor. Böyle bir inşa alalım ve bu inşadaki adım sayısına $n$ diyelim.

Her $0 \leq i \leq n$ için, $K_i$ kümesi, inşanın $i$ . adımı sonunda elde etmiş olduğumuz noktaların koordinatlarını içeren ve aritmetik işlemler altında kapalı gerçel sayıların en küçük alt kümesini belirtsin.

Burada aritmetik işlemler altında kapalı derken şunu kastediyoruz. Eğer $a$ ve $b$ kümenin elemanlarıysa, $a+b,a-b,ab$ ve $a/b$ sayıları da kümenin elemanlarıdır. Tabii sıfırla bölme yapmayı yasaklıyoruz. Dolayısıyla $b=0$ durumunda $a/b$ sayısının kümede olmasını beklemiyoruz. Yazının geri kalanında da aritmetik işlemler altında kapalı terminolojisini kullandığımızda bunu kastediyor olacağız. Cisim kavramının ne olduğunu bilenler için teknik terimlerle konuşmak gerekirse, $K_i$ kümesi $i$ . adım sonunda elde ettiğimiz tüm noktaların koordinatlarını içeren en küçük cisim.

İnşanın sıfırıncı adımında, yani henüz hiçbir temel işlem uygulamamışken, elimizde koordinatları $(0,0)$ ve $(1,0)$ olan iki nokta olduğu için $K_0=\mathbb{Q}$ olacaktır. Şimdi tüm dertlerimize derman olacak gözlem geliyor.

Önsav: Her $0 \leq i < n$ için

Ya $K_{i+1}=K_i$ olur, ya da
$K_{i+1}$ kümesi, $K_i$ kümesini ve $\sqrt{m} \notin K_i$ olan pozitif bir $m \in K_i$ sayısı için $\sqrt{m}$ sayısını içeren aritmetik işlemler altında kapalı en küçük kümedir.

Kanıt: Pergel ve cetvel inşalarını gerçekleştirmemizi sağlayan temel işlemlere bakalım. Bu temel işlemler arasından yeni noktalar elde etmemizi sağlayanlar sadece son üç işlem. Bu son üç işlemde yeni noktalar elde ederken o ana kadar elde ettiğimiz noktaları kullanarak oluşturabildiğimiz doğruları ve çemberleri kesiştiriyoruz. Demek ki inşanın $i+1$ . adımında elde edeceğimiz yeni nokta $i$ . adımda elimizde olan doğruları ve çemberleri kesiştirmemiz sonucu elde edilebilir.

$i$ . adım sonunda elimizde olan doğruların ve çemberlerin denklemlerini yazdığımızda bu denklemlerde göreceğimiz sabit terimler ve katsayılar $K_i$ kümesinin elemanı olmak zorundadır. Dolayısıyla bu çemberleri ve doğruları kesiştirdiğimizde elde edeceğimiz noktaların koordinatları, doğrular birinci derece ve çemberler ikinci derece denklemlerle ifade edildiği için, katsayıları $K_i$ kümesinde olan en fazla ikinci derece denklemlerin çözümlerinden gelecektir.

Eğer $i+1$ . adımda elde ettiğimiz yeni nokta iki doğru kesiştirilerek elde ediliyorsa, bu durumda bu noktanın koordinatları $K_i$ kümesinde olacaktır zira $K_i$ kümesi aritmetik işlemler altında kapalı. Eğer $i+1$ . adımda elde ettiğimiz yeni nokta bir çember ve bir doğrunun ya da iki çemberin kesişiminden elde ediliyorsa, ikinci derece denklemlerin çözüm formülü gereği bu noktanın koordinatları $K_i$ kümesindeki bir pozitif elemanın karekökü ve aritmetik işlemler yardımıyla elde edilebilir. Eğer ilgili diskriminantın karekökü $K_i$ kümesindeyse, bu durumda $K_i =K_{i+1}$ olacaktır. Eğer ilgili diskriminantın karekökü $K_i$ kümesinde değilse, bu durumda $K_{i+1}$ tanımı gereği teoremin ikinci maddesini sağlamak zorunda kalacaktır. $\blacksquare$ .

(Not: İki çemberi kesiştirdiğimiz zaman neden kesişim noktalarının koordinatlarını bulmak için ikinci derece bir denklem çözmenin yeterli olduğu bariz olmayabilir. Öte yandan elinize kalem kağıt alıp çözmeyi denerseniz böyle olması gerektiğini görebilirsiniz!)

Biliyoruz ki $n$ adım sonunda $(|r|,0)$ noktasını elde edebiliyoruz, yani $|r| \in K_{n}$ . Öte yandan, önsav gereği, her adımda elimizdeki noktaların koordinatlarını içeren en küçük cisim ya önceki adımda elde ettiğimiz cismin aynısı ya da önceki adımda elde ettiğimiz cisme bu cisimde karekökü olmayan pozitif bir elemanın karekökü eklenerek oluşturulmuş bir cisim. Demek ki her inşa edilebilir sayı bu şekilde elde edilebilmeli.

Biraz uğraşla bunun tersinin de doğru olduğunu gösterebilirsiniz. Yani öyle aritmetik işlemler altında kapalı $\mathbb{Q}=K_0 \subseteq K_1 \subseteq \dots \subseteq K_n$ kümeleri bulabiliyorsanız ki her küme bir önceki kümeden bu kümedeki pozitif bir elemanın karekökü eklenip aritmetik işlemler altında kapatılarak elde ediliyorsa, bu durumda en son kümedeki her sayı inşa edilebilirdir.

Kısaca inşa edilebilir sayılar, rasyonel sayılarla başlayıp her adımda daha önceki adımlarda elinizde olan sayılara aritmetik işlemler uygulayarak ve karekök alarak sonlu adımda elde edebileceğiniz sayılardır.

Bu noktada geniş halk kitlesi falan dinlemeyip kanıtladığımız teoremin matematiksel olarak doğru halini yazma gereği duyuyorum.

Teorem: Bir $r \in \mathbb{R}$ sayısı inşa edilebilirdir ancak ve ancak öyle bir $\mathbb{Q}=K_0 \subseteq K_1 \subseteq \dots \subseteq K_n$ cisim kulesi varsa ki $r \in K_n$ ve her $0 \leq i < n$ için $[K_{i+1}:K_i] \leq 2$ oluyorsa.

Çeşitli problemlerin çözümsüzlüğü

Yazının bu bölümünde saydığımız dört problemden ilk üçünün çözümü olmadığını göreceğiz. Bu problemlerin ne olduğunu hatırlayalım. Pergel ve cetvel ile

Bir çember verildiğinde bu çemberle aynı alana sahip bir kare çizmek.
Birim uzunluk verildiğinde $\sqrt[3]{2}$ uzunluğunu inşa etmek.
Bir açı verildiğinde bu açıyı üçe bölmek.

Eğer birinci problemi çözebiliyor olsaydık, birim yarıçapa sahip çemberin alanı $\sqrt{\pi}$ olduğu için, $\sqrt{\pi}$ sayısı inşa edilebilir olurdu. Eğer ikinci problemi çözebiliyor olsaydık, $\sqrt[3]{2}$ sayısı inşa edilebilir olurdu. Eğer üçüncü problemi çözebiliyor olsaydık, altmış dereceyi üçe bölerek yirmi dereceyi elde edebiliyor olurduk ve bunun sonucunda da $cos(\frac{\pi}{9})$ sayısı inşa edilebilir olurdu.

Öte yandan bu sayıların hiçbiri, bir önceki bölümde gördüğümüz teorem gereği, inşa edilebilir değildir. Dolayısıyla bu problemleri pergel ve cetvel kullanarak çözemeyiz. Peki bu sayılar neden önceki bölümde gördüğümüz teoremdeki inşa edilebilirlik koşulunu sağlamıyorlar?

Bu yazıyı planlarken bu bölüm için ne yapacağımı kestirememiştim, yazarken belki aklıma bir şeyler gelir umuduyla bodoslama yazmaya giriştim. Düşündüm, taşındım ve kanaat getirdim ki bu sayıların neden teoremdeki inşa edilebilirlik koşulunu sağlamadığını geniş halk kitlelerine temel cisim kuramı kavramlarını göstermeden anlatmak için bir yol yok.

Dolayısıyla bu noktada kaçınılmaz olandan kaçmayı bırakıp sizi otorite etkisine maruz bırakacağım. Bu sayıların hiçbiri inşa edilemezler çünkü değiller! Eğer bu sayıların neden yukarıdaki teoremdeki inşa edilebilirlik koşulunu sağlamadığını öğrenmeyi kafaya koyduysanız lisans seviyesinde cisim genişlemelerini anlatan herhangi bir soyut cebir kitabı sizin için yeterli olacaktır. Anahtar kelimeyi veriyorum: Minimal polinomlar.

Carl Friedrich Gauss ile Neşeli Saatler’de bu hafta: Düzgün çokgen çizmek

Yazının bu son bölümünde bir düzgün çokgenin pergel ve cetvelle ne zaman inşa edilebileceğini öğreneceğiz.

Eğer pergel ve cetvel kullanarak bir düzgün n-gen çizebiliyorsanız bu durumda $\frac{2\pi}{n}$ açısı, dolayısıyla da $cos(\frac{2\pi}{n})$ sayısı inşa edilebilir olmalı. Bunun tersi de doğru. Eğer $cos(\frac{2\pi}{n})$ sayısı inşa edilebilirse, bu durumda pergel ve cetvelle düzgün bir n-gen çizilebilir. Bu iddiaların kanıtları çok zor olmadığı için egzersiz olarak okuyucuya bırakıyorum.

Demek ki bir düzgün çokgenin pergel ve cetvelle inşa edilip edilemeyeceğini belirleyen şey $cos(\frac{2\pi}{n})$ sayısının inşa edilebilirliği.

Büyük insan Carl Friedrich Gauss henüz on dokuz yaşındayken bir düzgün 17-genin pergel ve cetvelle çizilebileceğini kanıtlıyor. Günlüğüne göre Gauss’u matematikçi olmaya iten temel sebeplerden biri de Antik Yunan’dan beri bilinen ve o zamana kadar çözülemeyen bu soruyu çözmüş olması. Hatta Gauss bu sonucunu o kadar seviyor ki mezartaşına bir 17-gen çizilmesini istiyor ama taş ustası bunun zorluğunu ve çizilse bile çembere yakın bir görüntü ortaya çıkacağını söyleyerek bunu yapmayı reddediyor.

Yukarıda inşa edilebilir sayıların rasyonel sayılarla başlayıp her adımda önceki adımlarda elde ettiğimiz sayılara aritmetik işlemler ve karekök işlemi uygulayarak elde edebileceğimiz sayılar olduğunu gördük. Eğer düzgün 17-gen pergel ve cetvelle inşa edilebilir bir çokgense, $cos(\frac{2\pi}{17})$ sayısı inşa edilebilir bir sayı olacağından bu şekilde elde edilebilmeli. $cos(\frac{2\pi}{17})$ değerinin ne olduğunu görmek istiyorsanız ilgili Wikipedia sayfasına bakabilirsiniz.

Şimdi de bir düzgün çokgenin pergel ve cetvelle ne zaman inşa edilebileceğini karakterize eden genel teoremi görelim.

Teorem (Gauss-Wantzel): $n \geq 3$ olmak üzere, bir düzgün $n$ -gen pergel ve cetvelle inşa edilebilirdir ancak ve ancak $n$ sayısı ya ikinin bir kuvvetiyse ya da asal çarpanlarına ayrıldığında farklı Fermat asalları $p_1,\dots,p_t$ için $n=2^k p_1 \dots p_t$ formundaysa.

Gauss ünlü kitabı Disquisitiones Arithmeticae‘da teoremdeki koşulun bir düzgün çokgenin pergel ve cetvelle çizilebilmesi için yeterli olduğunu kanıtlıyor. Bu koşulun gerekli olduğunu söylese de bunun kanıtını vermiyor. İlgili koşulun gerekli olduğunun kanıtı da daha sonra Pierre Wantzel tarafından veriliyor.

Yazıyı noktalarken pergel ve cetvelle nasıl düzgün 5-gen ve 17-gen inşa edilebileceğini gösteren iki tane .gif dosyası paylaşmak istiyorum.

pentagon_construct

Düzgün beşgen inşası

regular_heptadecagon_inscribed_in_a_circle

Düzgün on yedigen inşası

Not: Bu içerik ilk kez Can Numan müstear isimli matematik bölümü akademisyeni arkadaşımız tarafından kaleme alınmış olunmuş Taner Beyter tarafından sitemizi uyarlanmıştır.